


Sistemas Lineares
1. Definição de sistema linear
Um sistema linear é um conjunto de equações do 1° grau com duas ou mais incógnitas. As soluções de um sistema de equações são os valores das incógnitas que satisfazem simultaneamente todas as equações do sistema.
\begin{cases}
\begin{matrix}
a_{11}x_{1} & + & a_{12}x_{2} & + & ... & + & a_{1n}x_{n} & = & b_{1} \\
a_{21}x_{1} & + & a_{22}x_{2} & + & ... & + & a_{2n}x_{n} & = & b_{2} \\
\vdots & & \vdots & & \vdots & & \vdots & & \vdots \\
a_{m1}x_{1} & + & a_{m2}x_{2} & + & ... & + & a_{mn}x_{n} & = & b_{m} \\
\end{matrix}
\end{cases}
2. Métodos de resolução de sistemas lineares
Os métodos mais comuns utilizados são:
Método da adição
Consiste na adição membro a membro das equações com a finalidade de calcular uma das variáveis.
Exemplo:
\begin{cases}
x+y=8 \\
x-2y=-1 \\
\end{cases}
Vamos multiplicar por $(-1)$ a segunda equação para possibilitar a eliminação da variável $x$;
$x + y = 8$
$-x + 2y = 1$
Agora somando membro a membro as duas equações, eliminaremos a variável $x$, possibilitando o cálculo da variável $y$:
$3y = 9$; portanto $y = 3$
Vamos substituir o valor da variável $y$ na primeira equação para calcularmos a variável $x$:
$x + 3 = 8$; portanto $x = 5$
Solução: $ \ x = 5$ ; $y = 3$
Método da substituição
Esse método consiste em escolhermos uma das equações para isolarmos uma variável e substituí-la na outra equação.
Exemplo:
\begin{cases}
x+2y=1 \\
2x+y=5 \\
\end{cases}
Isolando a variável $x$ na primeira equação obtemos:
$x = 1 - 2y$
Substituindo na segunda equação para calcularmos o valor de $y$:
$2.(1 - 2y) + y = 5$
$2 \hspace{0.2em} - 4y + y = 5$
$- 4y + y = 5 \hspace{0.2em} - 2$
$-3y = 3$
$3y = -3$ ; portanto $y = -1$
Substituindo o valor de $y$ na primeira equação obteremos:
$x + 2.(-1) = 1$
$x = 1 +2$ ; portanto $x = 3$
Solução: $ \ x = 3$ ; $y = -1$
3. Regra de Cramer
A regra de Cramer é uma das maneiras de resolver um sistema linear, mas só poderá ser utilizada na resolução de sistemas que tenham o número de equações $n$ igual ao de variáveis $n$.
Considerando o sistema linear abaixo:
\begin{cases}
\begin{matrix}
a_{11}x_{1} & + & a_{12}x_{2} & + & ... & + & a_{1n}x_{n} & = & b_{1} \\
a_{21}x_{1} & + & a_{22}x_{2} & + & ... & + & a_{2n}x_{n} & = & b_{2} \\
\vdots & & \vdots & & \vdots & & \vdots & & \vdots \\
a_{n1}x_{1} & + & a_{n2}x_{2} & + & ... & + & a_{nn}x_{n} & = & b_{n} \\
\end{matrix}
\end{cases}
Podemos representa-lo matricialmente na forma $A.B = C$ conforme abaixo:
\[
\begin{bmatrix}
a_{11} & a_{12} & ... & a_{1n} \\
a_{21} & a_{22} & ... & a_{2n} \\
\vdots & \vdots & \vdots & \vdots \\
a_{n1} & a_{n2} & ... & a_{nn} \\
\end{bmatrix}
.
\begin{bmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{n} \\
\end{bmatrix}
=
\begin{bmatrix}
b_{1} \\
b_{2} \\
\vdots \\
b_{n} \\
\end{bmatrix}
\]
A matriz $A$ formada com os coeficientes das equações lineares é chamada de matriz incompleta.
Para o cálculo das variáveis utilizamos a seguinte fórmula:
$x_{i} = \dfrac{det(A_{x_{i}})}{det(A)} \qquad $ ( com $i$ variando de $1$ a $n$ )
Por exemplo, para obtermos a matriz $A_{{x}_{1}}$ devemos substituir a 1ª coluna da matriz $A$, que contém os coeficientes de $x_{1}$, pela coluna da matriz $C$, que são os termos independentes das equações.
\[
A_{x_{1}} =
\begin{bmatrix}
b_{1} & a_{12} & ... & a_{1n} \\
b_{2}& a_{22} & ... & a_{2n} \\
\vdots & \vdots & \vdots & \vdots \\
b_{n} & a_{n2} & ... & a_{nn} \\
\end{bmatrix}
\hspace{2em}
(\text{matriz da incógnita} \ x_{1})
\]
Exemplo 1:
Calcule o valor de $x$ e $y$ do sistema de equações abaixo:
\begin{cases}
x+2y=1 \\
2x+y=5 \\
\end{cases}
Pela regra de Cramer matricialmente temos $A.B = C$:
\[
\begin{bmatrix}
1 & 2 \\
2 & 1 \\
\end{bmatrix}
.
\begin{bmatrix}
x \\
y \\
\end{bmatrix}
=
\begin{bmatrix}
1 \\
5 \\
\end{bmatrix}
\]
 $det(A_{x}) = 1.(-1).(-1) + 1.(-3).(1) + 1.2.(1) \hspace{0.2em} - 1.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$
$det(A_{x}) = 1 - 3 + 2 + 1 + 3 + 2$
$det(A_{x}) = 6$
$det(A_{x}) = 1.(-1).(-1) + 1.(-3).(1) + 1.2.(1) \hspace{0.2em} - 1.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$
$det(A_{x}) = 1 - 3 + 2 + 1 + 3 + 2$
$det(A_{x}) = 6$
 $det(A_{y}) = 1.2.(-1) + 1.(-3).(2) + 1.2.1 - 2.2.1 - 1.(-3).1 - (-1).2.1$
$det(A_{y}) = - 2 - 6 + 2 - 4 + 3 + 2$
$det(A_{y}) = - 5$
$det(A_{y}) = 1.2.(-1) + 1.(-3).(2) + 1.2.1 - 2.2.1 - 1.(-3).1 - (-1).2.1$
$det(A_{y}) = - 2 - 6 + 2 - 4 + 3 + 2$
$det(A_{y}) = - 5$
 $det(A_{z}) = 1.(-1).1 + 1.2.2 + 1.2.1 - 2.(-1).1 - 1.2.1 - 1.2.1$
$det(A_{z}) = - 1 + 4 + 2 + 2 - 2 - 2$
$det(A_{z}) = 3$
Finalmente vamos calcular o valor de $x$, $y$ e $z$:
$det(A_{z}) = 1.(-1).1 + 1.2.2 + 1.2.1 - 2.(-1).1 - 1.2.1 - 1.2.1$
$det(A_{z}) = - 1 + 4 + 2 + 2 - 2 - 2$
$det(A_{z}) = 3$
Finalmente vamos calcular o valor de $x$, $y$ e $z$:
$x=\dfrac{det(A_{x})}{det(A)}$
$y=\dfrac{det(A_{y})}{det(A)}$
Vamos calcular o valor do determinante da matriz incompleta:
\[
det(A) =
\begin{vmatrix}
1 & 2 \\
2 & 1 \\
\end{vmatrix}
=
1.1-2.2=1-4
\]
$ \hspace{-7.8em} det(A)=-3$
A matriz $A_{x}$ é obtida com a substituição da 1ª coluna da matriz $A$, que contém os coeficientes de $x$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:
\[
A_{x} =
\begin{bmatrix}
1 & 2 \\
5 & 1 \\
\end{bmatrix}
\]
A matriz $A_{y}$ é obtida com a substituição da 2ª coluna da matriz $A$, que contém os coeficientes de $y$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:
\[
A_{y} =
\begin{bmatrix}
1 & 1 \\
2 & 5 \\
\end{bmatrix}
\]
Vamos calcular os determinantes $det(A_{x})$ e $det(A_{y})$.
\[
det(A_{x}) =
\begin{vmatrix}
1 & 2 \\
5 & 1 \\
\end{vmatrix}
= 1.1-5.2=1-10
\]
$\hspace{-8.3em} det(A_{x})=-9$
\[
\hspace{-0.3em}
det(A_{y}) =
\begin{vmatrix}
1 & 1 \\
2 & 5 \\
\end{vmatrix}
= 1.5-2.1=5-2
\]
$\hspace{-4em} det(A_{y})=3$
$x=\dfrac{det(A_{x})}{det(A)}=\dfrac{-9}{-3}$
$x=3$
$y=\dfrac{det(A_{y})}{det(A)}=\dfrac{3}{-3}$
$y=-1$
Solução: $ \ x=3$; $y=-1$
Exemplo 2:
Calcule o valor de $x$, $y$ e $z$ do sistema de equações abaixo:
\begin{cases}
x+y+z=1 \\
2x-y-3z=2 \\
2x+y-z=1 \\
\end{cases}
Pela regra de Cramer matricialmente temos $A.B = C$:
\[
\begin{bmatrix}
1 & 1 & 1 \\
2 & -1 & -3 \\
2 & 1 & -1 \\
\end{bmatrix}
.
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
=
\begin{bmatrix}
1 \\
2 \\
1 \\
\end{bmatrix}
\]
$x=\dfrac{det(A_{x})}{det(A)}$
$y=\dfrac{det(A_{y})}{det(A)}$
$z=\dfrac{det(A_{z})}{det(A)}$
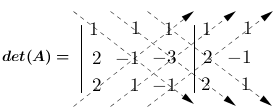
Vamos calcular o determinante da matriz incompleta utilizando a regra de Sarrus:

$det(A) = 1.(-1).(-1) + 1.(-3).2 + 1.2.1 \hspace{0.2em} - 2.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$
$det(A) = 1 - 6 + 2 + 2 + 3 + 2$
$det(A) = 4$
A matriz $A_{x}$ é obtida com a substituição da 1ª coluna da matriz $A$, que contém os coeficientes de $x$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:
\[
A_{x} =
\begin{bmatrix}
1 & 1 & 1 \\
2 & -1 & -3 \\
1 & 1 & -1 \\
\end{bmatrix}
\]
A matriz $A_{y}$ é obtida com a substituição da 2ª coluna da matriz $A$, que contém os coeficientes de $y$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:
\[
A_{y} =
\begin{bmatrix}
1 & 1 & 1 \\
2 & 2 & -3 \\
2 & 1 & -1 \\
\end{bmatrix}
\]
A matriz $A_{z}$ é obtida com a substituição da 3ª coluna da matriz $A$, que contém os coeficientes de $z$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:
\[
A_{z} =
\begin{bmatrix}
1 & 1 & 1 \\
2 & -1 & 2 \\
2 & 1 & 1 \\
\end{bmatrix}
\]
Vamos calcular os determinantes $det(A_{x})$, $det(A_{y})$ e $det(A_{z})$.
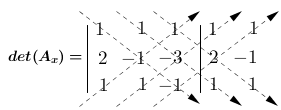
 $det(A_{x}) = 1.(-1).(-1) + 1.(-3).(1) + 1.2.(1) \hspace{0.2em} - 1.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$
$det(A_{x}) = 1 - 3 + 2 + 1 + 3 + 2$
$det(A_{x}) = 6$
$det(A_{x}) = 1.(-1).(-1) + 1.(-3).(1) + 1.2.(1) \hspace{0.2em} - 1.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$
$det(A_{x}) = 1 - 3 + 2 + 1 + 3 + 2$
$det(A_{x}) = 6$
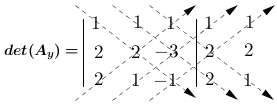
 $det(A_{y}) = 1.2.(-1) + 1.(-3).(2) + 1.2.1 - 2.2.1 - 1.(-3).1 - (-1).2.1$
$det(A_{y}) = - 2 - 6 + 2 - 4 + 3 + 2$
$det(A_{y}) = - 5$
$det(A_{y}) = 1.2.(-1) + 1.(-3).(2) + 1.2.1 - 2.2.1 - 1.(-3).1 - (-1).2.1$
$det(A_{y}) = - 2 - 6 + 2 - 4 + 3 + 2$
$det(A_{y}) = - 5$
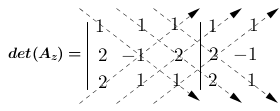
 $det(A_{z}) = 1.(-1).1 + 1.2.2 + 1.2.1 - 2.(-1).1 - 1.2.1 - 1.2.1$
$det(A_{z}) = - 1 + 4 + 2 + 2 - 2 - 2$
$det(A_{z}) = 3$
Finalmente vamos calcular o valor de $x$, $y$ e $z$:
$det(A_{z}) = 1.(-1).1 + 1.2.2 + 1.2.1 - 2.(-1).1 - 1.2.1 - 1.2.1$
$det(A_{z}) = - 1 + 4 + 2 + 2 - 2 - 2$
$det(A_{z}) = 3$
Finalmente vamos calcular o valor de $x$, $y$ e $z$:
$x=\dfrac{det(A_{x})}{det(A)}=\dfrac{6}{4}$
$x=1,5$
$y=\dfrac{det(A_{y})}{det(A)}=\dfrac{-5}{4}$
$y=-1,25$
$z=\dfrac{det(A_{z})}{det(A)}=\dfrac{3}{4}$
$z=0,75$
Solução: $ \ x = 1,5$; $y = -1,25$; $z = 0,75$.
4. Classificação e análise de um sistema linear
De acordo com o número de soluções que um sistema possui podemos classificá-lo como:
1 - Sistema Possível (SP):
Quando admite pelo menos uma solução. O sistema possível subdivide-se em:
1.1 - Sistema Possível e Determinado (SPD): Quando admite apenas uma solução.
1.2 - Sistema Possível e Indeterminado (SPI): Quando admite infinitas soluções.
2 - Sistema Impossível (SI): Quando não possui solução.
Calculando o determinante de uma matriz incompleta $(det(A))$ podemos afirmar que:
- Se o $det(A)$ for diferente de zero, o Sistema é Possível e Determinado (SPD).
- Se o $det(A)$ for igual a zero, o Sistema é Impossível (SI) ou Possível e Indeterminado (SPI). Exclui a possibilidade de ser Sistema Possível e Determinado (SPD).
5. Sistemas homogêneos
Um sistema é homogêneo quando todos os termos independentes forem iguais a zero.
Exemplo:
\begin{cases}
x+3y=0 \\
2x+4y=0 \\
\end{cases}
\begin{cases}
x+3y=0 \\
2x+6y=0 \\
\end{cases}
Observamos que uma solução para os sistemas é $x=0$ e $y=0$, que é chamada de solução trivial, nula ou imprópria. Portanto podemos afirmar que todo sistema homogêneo é sempre possível (SP).
Analisando o primeiro sistema de equações verificamos que o determinante da matriz incompleta é diferente de zero $(det(A)= -2)$, portanto o Sistema é Possível e Determinado (SPD).
No segundo sistema de equações verificamos que o determinante da matriz incompleta é igual a zero $(det(A)= 0)$, portanto o sistema é Possível e Indeterminado (SPI).



